BANDの特長
 様々な系に適用可能な高精度バンド計算ソフトウェア
様々な系に適用可能な高精度バンド計算ソフトウェア
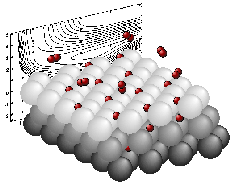
BANDは、ポリマー、表面、バルク結晶などの研究を目的とした周期系を取り扱う密度汎関数法ソフトウェアです。擬ポテンシャル近似は用いず、全電子計算またはFrozen Core近似を使用した高精度な計算が可能です。BANDは、平面波を基底関数として採用する多くのバンド計算プログラムとは異なり、1〜2次元の周期境界条件を課すことが可能で、真のスラブ近似を使用した効率的な計算が可能です。基底関数には原子軌道(数値型+Slater型)を採用しており、周期表の全元素に対応した基底関数を完備しています。また、姉妹プログラムであるADFと同じ相対論法を搭載しているため、重原子を含む様々な系に適用可能です。
 原子軌道の特徴を活かしたプロパティ計算・解析機能
原子軌道の特徴を活かしたプロパティ計算・解析機能
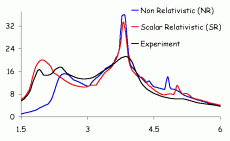
BANDは、基底関数として原子軌道を採用しているため、部分状態密度や原子電荷など、原子に帰属させるプロパティの計算に適しています。不均一触媒の研究にしばしば使用され、金属表面への化学吸着や化学反応のポテンシャルエネルギー曲面の解析に応用されています。BANDでは、様々な交換相関汎関数が使用でき、結合(凝集)エネルギー解析、Mullikenポピュレーション解析、電荷密度フーリエ解析(構造因子)が可能です。また、フラグメント解析機能の特徴から、各フラグメントの分子軌道を用いた状態密度データの分割を行うことができます。さらに、時間依存密度汎関数法(TD-DFT)による精度の高い周波数依存誘電関数の計算や、周期系に対するNMR・ESR計算が可能です。
BANDの機能
 計算方法
計算方法
- 密度汎関数法: LDA, GGA(BP, PW91, BLYP, PBE, PBEsol, etc.), GGA-D(D, D3, D3(BJ)), Meta-GGA(MO6L, TPSS, etc.), model(LB94, TB-mBJ), LDA+U
- 相対論効果: Scalar(ZORA), Spin-Orbit(ZORA)
- 溶媒効果: COSMO
- 外場の設定: 一様な静電場(1〜2次元)
 構造予測・反応解析
構造予測・反応解析
- 構造最適化計算: quasi-Newton
- 遷移状態探索: EF
 プロパティ計算
プロパティ計算
- バンド構造
- 状態密度: 全状態密度、部分状態密度、局所状態密度
- 原子電荷: Mulliken, Hirshfeld, Voronoi
- 数値微分による振動数計算
- フォノン分散、熱力学物性(比熱、自由エネルギー)
- 周波数依存誘電関数: バンド間遷移とバンド内遷移の両方に対応
- 電子エネルギー損失分光スペクトル(EELS)
- NMR: 化学テンソル
- ESR: gテンソル、Aテンソル、NQCC(EFG)、Qテンソル
 解析機能
解析機能
- 結合エネルギー解析
- 電荷密度フーリエ解析
- AIM, ELF
 精度・効率
精度・効率
- 数値型+Slater型の原子基底関数: 周期表の全元素に対応した全電子基底関数およびFrozen Core基底関数を完備
- te Velde-Baerendsの数値積分スキーム1 を用いた効率のよい数値積分
1) P. M. Boerrigter, G. te Velde, and E. J. Baerends, lnt. J. Quantum Chem. 33, 87 (1988).
G. te Velde and E. J. Baerends, J. Comput. Phys. 99, 84 (1992).
- 電子密度フィッティングによるクーロン相互作用の高速化
 様々な系に適用可能な高精度バンド計算ソフトウェア
様々な系に適用可能な高精度バンド計算ソフトウェア BANDは、ポリマー、表面、バルク結晶などの研究を目的とした周期系を取り扱う密度汎関数法ソフトウェアです。擬ポテンシャル近似は用いず、全電子計算またはFrozen Core近似を使用した高精度な計算が可能です。BANDは、平面波を基底関数として採用する多くのバンド計算プログラムとは異なり、1〜2次元の周期境界条件を課すことが可能で、真のスラブ近似を使用した効率的な計算が可能です。基底関数には原子軌道(数値型+Slater型)を採用しており、周期表の全元素に対応した基底関数を完備しています。また、姉妹プログラムであるADFと同じ相対論法を搭載しているため、重原子を含む様々な系に適用可能です。
BANDは、ポリマー、表面、バルク結晶などの研究を目的とした周期系を取り扱う密度汎関数法ソフトウェアです。擬ポテンシャル近似は用いず、全電子計算またはFrozen Core近似を使用した高精度な計算が可能です。BANDは、平面波を基底関数として採用する多くのバンド計算プログラムとは異なり、1〜2次元の周期境界条件を課すことが可能で、真のスラブ近似を使用した効率的な計算が可能です。基底関数には原子軌道(数値型+Slater型)を採用しており、周期表の全元素に対応した基底関数を完備しています。また、姉妹プログラムであるADFと同じ相対論法を搭載しているため、重原子を含む様々な系に適用可能です。
 原子軌道の特徴を活かしたプロパティ計算・解析機能
原子軌道の特徴を活かしたプロパティ計算・解析機能 BANDは、基底関数として原子軌道を採用しているため、部分状態密度や原子電荷など、原子に帰属させるプロパティの計算に適しています。不均一触媒の研究にしばしば使用され、金属表面への化学吸着や化学反応のポテンシャルエネルギー曲面の解析に応用されています。BANDでは、様々な交換相関汎関数が使用でき、結合(凝集)エネルギー解析、Mullikenポピュレーション解析、電荷密度フーリエ解析(構造因子)が可能です。また、フラグメント解析機能の特徴から、各フラグメントの分子軌道を用いた状態密度データの分割を行うことができます。さらに、時間依存密度汎関数法(TD-DFT)による精度の高い周波数依存誘電関数の計算や、周期系に対するNMR・ESR計算が可能です。
BANDは、基底関数として原子軌道を採用しているため、部分状態密度や原子電荷など、原子に帰属させるプロパティの計算に適しています。不均一触媒の研究にしばしば使用され、金属表面への化学吸着や化学反応のポテンシャルエネルギー曲面の解析に応用されています。BANDでは、様々な交換相関汎関数が使用でき、結合(凝集)エネルギー解析、Mullikenポピュレーション解析、電荷密度フーリエ解析(構造因子)が可能です。また、フラグメント解析機能の特徴から、各フラグメントの分子軌道を用いた状態密度データの分割を行うことができます。さらに、時間依存密度汎関数法(TD-DFT)による精度の高い周波数依存誘電関数の計算や、周期系に対するNMR・ESR計算が可能です。
 計算方法
計算方法 構造予測・反応解析
構造予測・反応解析 プロパティ計算
プロパティ計算 解析機能
解析機能 精度・効率
精度・効率