遷移金属錯体は、18電子則を満たす化合物が安定であることが経験的に知られています。一方、fブロック元素（ランタノイド、アクチノイド）を含む化合物は、18電子則の類推から必然的に、32電子則を満たす化合物が安定であることが予想されます。最近、Dognonら^{1, 2}は、一連のアクチノイド化合物に対してADFを使用したDFT計算を行うことにより、32電子則を満たす化合物の安定性を確かめました。

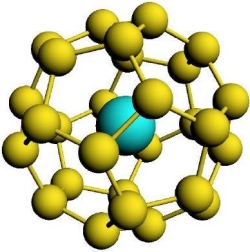
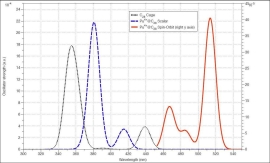
彼らは、エネルギー計算による分子の安定性評価の他に、IRやUV/Visなどのスペクトル計算も行っています。上図は、C28フラーレンに内包されたPu⁴⁺の系（左）とそのUV/Visスペクトル（右）を表示したものです。UV/Visスペクトルは、スピン-軌道相互作用を考慮した相対論とスカラー相対論の場合とで比較されていますが、このようなアクチノイド化合物に対してはスピン-軌道相互作用の効果が非常に重要であることがわかります。ADFでは、ZORA法と呼ばれる相対論法が実装されており、スピン-軌道相互作用を考慮した計算が可能です。

1) J. P. Dognon et al., Angew. Chem. Int. Ed., 46, 1427 (2007).
2) J. P. Dognon et al., J. Am. Chem. Soc., 131, 238 (2009).

ADFの特長の一つとして、基底関数として一般的なGauss型ではなくSlater型の軌道を採用することで精度の高い計算を実現していることが挙げられます。
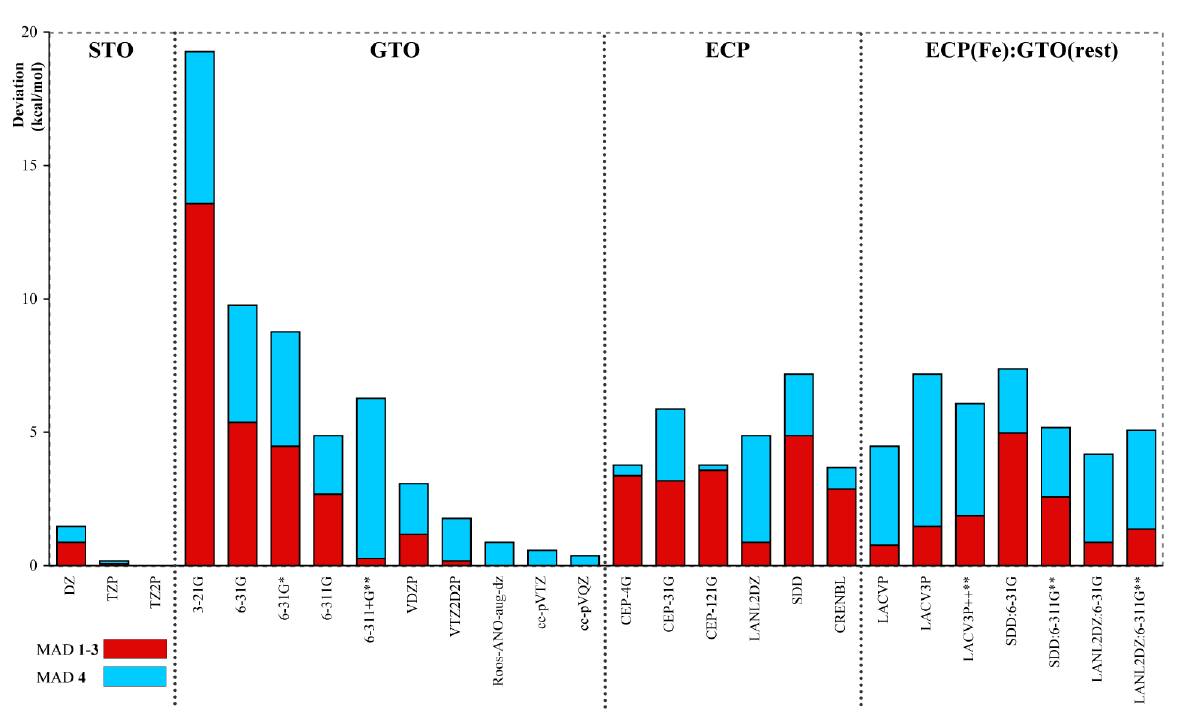
Güellら¹は、ニトリルへドラターゼ（Nhase）のモデル錯体を始めとする一連の鉄錯体に対して、スピン状態間のエネルギー差の基底関数依存性をSlater型軌道（STO）とGauss型軌道（GTO）で比較しました。

GTO基底では収束が遅い

STO基底とGTO基底による結果は、それぞれの基底関数の規模を大きくしていく極限において一致します。しかし、STO基底がTZP規模ですでに収束しているのと比べると、GTO基底の収束が遅いのがわかります。彼らは、その要因として、原子核付近での正確な記述（カスプの再現）を可能にするSTOの優位性を指摘しています。

ECP基底では収束しない

ECP基底を使用した計算では、内殻電子の効果をポテンシャルに置き換えて計算しています。そのため、その結果がSTOやGTOなどの全電子基底の結果と一致するとは限りません。実際、ECP法に基づく計算では、かなり大きな基底関数系を用いた場合でもその結果が収束していないことがわかります。

このように、真の原子軌道の特徴（カスプと指数関数的な減衰）を再現するSTOを基底関数として採用することで、小さい規模の基底でも正しい結果が得られることが期待されます。

1) M. Güell et al., J. Phys. Chem. A, 112, 6384 (2008).

各基底関数の平均絶対誤差（kcal/mol）