ADFの特長
 様々な系に適用可能な密度汎関数法ソフトウェア
様々な系に適用可能な密度汎関数法ソフトウェア
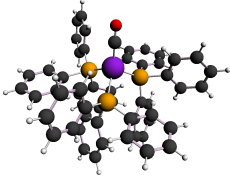
Amsterdam Density Functional (ADF)は、密度汎関数法(DFT)に基づく量子化学計算ソフトウェアで、均一系、不均一系触媒から無機化学、重元素化学、生化学、各種分光学まで幅広い分野の研究に利用されています。DFTは、1990年代初頭から広く使われるようになった方法で、電子相関を含んでいる点でHartree-Fock法よりも高精度です。また、post Hartree-Fock法(MP2, CI, CCなど)では取り扱いが困難なサイズである数百原子からなる化合物についても高速に計算することができます。ADFは遷移金属を含んだ系でもSCF計算の収束がよく、重元素系で重要な相対論の効果を含めることができます。さらに、周期表の全元素に対応した全電子計算用の基底関数(Slater型)を完備していることは、ADFの大きな特長の一つです。
 豊富なプロパティ計算機能
豊富なプロパティ計算機能
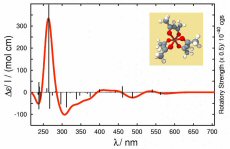
ADFは種々の分子物性を高精度に計算することができます。時間依存密度汎関数法(TD-DFT)により、紫外・可視吸収スペクトル(振動子強度と一重項・三重項励起エネルギー)や、周波数依存分極率、ラマン強度、ファン・デル・ワールス分散係数などを計算します。また、IRの振動数や強度、多重極子モーメントと同様に、NMRの化学シフトやスピン-スピンカップリング、ESR(EPR) g-テンソル、磁気的・電気的超微細構造テンソル、核四重極子カップリング定数の計算が可能です。ほとんどの物性計算に対して相対論の効果を考慮した計算を行うことができます。
ADFの機能
 計算方法
計算方法
- Hartree-Fock法: RHF, UHF
- 密度汎関数法: LDA, Xα
GGA (BP, PW91, mPW, BLYP, PBE, RPBE, revPBE, mPBE, OLYP, OPBE)
Hybrid (B3LYP, O3LYP, BHandHLYP, B1PW91, MPW1PW, MPW1K, PBE0, OPBE0, etc.)
(hybrid) meta-GGA (KCIS, VS98, FT97, BLAP3, BOP, OLAP3, TPSS, TPSSh, B97, M05, M06, etc.)
MM Dispersion corrected (BLYP-D, PBE-D, BP86-D, TPSS-D, B3LYP-D, B97-D)
Model (SAOP, GRAC, LB94)
- 相対論効果: Scalar (ZORA), Spin-Orbit (ZORA)
- 溶媒効果: COSMO, DRF, SCRF, 3D-RISM, DFT/DFT
- 外場の設定: 点電荷、静電場、non-self-consistent Green’s function計算
- QM/MM: IMOMM/ADF, AddRemove, QUILD
- 分子動力学計算: マルチスケールMD, Biased MD(メタダイナクミス、アンブレラサンプリングなど)
 構造予測・反応解析
構造予測・反応解析
- 構造最適化計算: quasi-Newton
- 遷移状態探索: EF, NEB
- 反応経路: Linear Transit, IRC
 プロパティ計算
プロパティ計算
- 熱力学物性: エントロピー、モル比熱など
- IRスペクトル、(共鳴)ラマンスペクトル、振動ラマン光学活性(VROA)、Franck-Condon因子
- 紫外・可視吸収スペクトル、X線吸収スペクトル
- 円二色性スペクトル(VCD, ECD)、旋光分散スペクトル(ORD)
- 磁気円二色性スペクトル(MCD)、Verdet定数、Faraday A, B項
- NMR: 化学シフト、スピン-スピンカップリング
- ESR: gテンソル、Aテンソル、ZFS、NQCC(EFG)、Qテンソル
- メスバウアースペクトル、NRVSスペクトル
- 電気的多重極子モーメント、(周波数依存)分極率・超分極率、(動的)磁化率
- ファン・デル・ワールス分散係数
- 原子電荷: Mulliken, Hirshfeld, Voronoi, AIM
- 輸送特性: charge transfer integral
 解析機能
解析機能
- フラグメント軌道による相互作用解析: フラグメントはユーザ定義が可能
- 結合エネルギー解析、ETS-NOCV
- 結合次数解析: Mayer, Nalewajski-Mrozek
 精度・効率
精度・効率
- Slater型軌道による原子基底関数:周期表の全元素に対応した全電子基底関数およびFrozen Core基底関数を完備
- te Velde-Baerendsの数値積分スキーム1を用いた効率のよい数値積分
1) P. M. Boerrigter, G. te Velde, and E. J. Baerends, lnt. J. Quantum Chem. 33, 87 (1988).
G. te Velde and E. J. Baerends, J. Comput. Phys. 99, 84 (1992).
- 電子密度フィッティングによるクーロン相互作用の高速化
- 基底関数のカットオフ: O(N)
 様々な系に適用可能な密度汎関数法ソフトウェア
様々な系に適用可能な密度汎関数法ソフトウェア Amsterdam Density Functional (ADF)は、密度汎関数法(DFT)に基づく量子化学計算ソフトウェアで、均一系、不均一系触媒から無機化学、重元素化学、生化学、各種分光学まで幅広い分野の研究に利用されています。DFTは、1990年代初頭から広く使われるようになった方法で、電子相関を含んでいる点でHartree-Fock法よりも高精度です。また、post Hartree-Fock法(MP2, CI, CCなど)では取り扱いが困難なサイズである数百原子からなる化合物についても高速に計算することができます。ADFは遷移金属を含んだ系でもSCF計算の収束がよく、重元素系で重要な相対論の効果を含めることができます。さらに、周期表の全元素に対応した全電子計算用の基底関数(Slater型)を完備していることは、ADFの大きな特長の一つです。
Amsterdam Density Functional (ADF)は、密度汎関数法(DFT)に基づく量子化学計算ソフトウェアで、均一系、不均一系触媒から無機化学、重元素化学、生化学、各種分光学まで幅広い分野の研究に利用されています。DFTは、1990年代初頭から広く使われるようになった方法で、電子相関を含んでいる点でHartree-Fock法よりも高精度です。また、post Hartree-Fock法(MP2, CI, CCなど)では取り扱いが困難なサイズである数百原子からなる化合物についても高速に計算することができます。ADFは遷移金属を含んだ系でもSCF計算の収束がよく、重元素系で重要な相対論の効果を含めることができます。さらに、周期表の全元素に対応した全電子計算用の基底関数(Slater型)を完備していることは、ADFの大きな特長の一つです。
 豊富なプロパティ計算機能
豊富なプロパティ計算機能 ADFは種々の分子物性を高精度に計算することができます。時間依存密度汎関数法(TD-DFT)により、紫外・可視吸収スペクトル(振動子強度と一重項・三重項励起エネルギー)や、周波数依存分極率、ラマン強度、ファン・デル・ワールス分散係数などを計算します。また、IRの振動数や強度、多重極子モーメントと同様に、NMRの化学シフトやスピン-スピンカップリング、ESR(EPR) g-テンソル、磁気的・電気的超微細構造テンソル、核四重極子カップリング定数の計算が可能です。ほとんどの物性計算に対して相対論の効果を考慮した計算を行うことができます。
ADFは種々の分子物性を高精度に計算することができます。時間依存密度汎関数法(TD-DFT)により、紫外・可視吸収スペクトル(振動子強度と一重項・三重項励起エネルギー)や、周波数依存分極率、ラマン強度、ファン・デル・ワールス分散係数などを計算します。また、IRの振動数や強度、多重極子モーメントと同様に、NMRの化学シフトやスピン-スピンカップリング、ESR(EPR) g-テンソル、磁気的・電気的超微細構造テンソル、核四重極子カップリング定数の計算が可能です。ほとんどの物性計算に対して相対論の効果を考慮した計算を行うことができます。
 計算方法
計算方法 構造予測・反応解析
構造予測・反応解析 プロパティ計算
プロパティ計算 解析機能
解析機能 精度・効率
精度・効率